一、问题情境

圆对于我们并不陌生，在小学，曾经学习过有关圆的面积的计算，我们来看下面的面积问题：

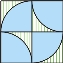
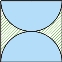
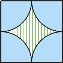
1.下图中各个正方形的边长都相等，其中的曲线都是圆弧的一部分，你能说明它们阴影部分的面积都相等吗？

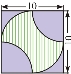
2. 下图阴影部分是以正方形边长的一半为半径的圆弧围成的（斯坦因豪斯图形），你能求出阴影部分的面积吗？

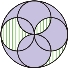3. 下图4个小圆的面积相等，大圆的半径等于小圆的直径，你能判断图中阴影部分的面积与大圆面积的关系吗？

本章将在小学的基础上，经一步研究圆的性质，探索点与圆、直线与圆、圆与圆的位置关系。

二、问题情境

1. 在日常生活中，我们见到的汽车、摩托车、自行车等交通工具的车轮是什么形状，你能说明车轮为什么做成这种形状吗？如果改成其他形状（如正方形、三角形）会发生怎样的情况？

2. 将线段OP的一个端点O固定，使线段OP绕着点O在平面内旋转1周，观察另一个端点P运动形成的图形。点P在运动的过程中，与点O的距离是否始终相等？

三、知识归纳

将线段OP的一个端点O固定，使线段OP绕着点O在平面内旋转1周，观察另一个端点P运动形成的图形叫做圆。其中定点O 叫做圆心，线段OP叫做半径。

 以O 为圆心的圆，记作“⊙ O”，读作“圆O”。

四、探索研究

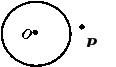1.在平面内，点与圆有几种位置关系？

点在圆内               点在圆上            点在圆外

2.并比较圆内的点、圆上的点、圆外的点到圆心的距离与半径的大小。你发现了什么？

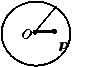
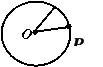
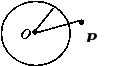
OP＜r                   OP=r               OP＞r

五、知识归纳

1. 圆上各点到圆心（定点）的距离都等于半径（定长）；到圆心距离等于半径的点在圆上.

即 圆是到定点距离等于定长的点的集合.

同理： 圆的内部可以看作到圆心距离小于半径的点的集合.

同理： 圆的外部可以看作到圆心距离大于半径的点的集合.

2. 如果⊙ O的半径为r,点P到圆心O的距离为d,那么

点P在圆内       d＜r

点P在圆上       d＝r

点P在圆外       d＞r

六、例题讲解

例1  如图，已知点P、Q，且PQ＝4cm.

（1）画出下列图形

到点P的距离等于2cm的点的集合；

到点Q的距离等于3cm的点的集合.

（2）在所画图中，到点P的距离等于2cm，且到点Q的距离等于3cm的点有几个？请在图中将它们表示出来.

（3）在所画图中，到点P的距离小于或等于2cm，且到点Q的距离大于或等于3cm的点的集合是怎样的图形？把它画出来.

例2 已知：如图，菱形ABCD的对角线AC、BD相交于点O，E、F、G、H分别是AB、BC、CD、DA的中点.试说明点E、F、G、H在以点O为圆心的同一个圆上。

七、课堂练习

课本P108 1，2，3。

六、拓展提高

若⊙O的半径是5cm，点O到直线l的距离OD＝3cm.点A、B、C在直线l上.且AD ＝     cm, BD ＝ 4 cm,CD ＝     cm,则点A在⊙O         ，点B在⊙O         ，点C在⊙O          .

八、小结与思考：

通过这节课的学习你有哪些收获与困惑？

九．布置作业：